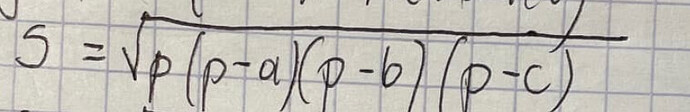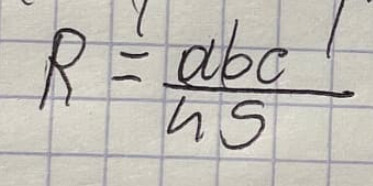Tak, zgadza się. Brałem to po uwagę, ( że tak może być), ale że nie ma to wpływu na wynik, to sobie około północy nie zawracałem już tym głowy. Niemniej masz jak najbardziej rację.
2 polubienia
Skorzystaliśmy z tego samego Herona,
jednak jako połowę obwodu trójkąta abc dalimy nie 7,5 a (piętnaście drugich) 15/2
Pole trójkąta abc wylazło zatem pierwiastek z ( 1575 / 16 )
P = √(1575/16)
Tę wartość podstawiliśmy do wzoru na promień okręgu opisanego na trójkącie 4, 5, 6
i wylazło
120 / 4√(1575/16)
120 podzielone przez czterokrotność pierwiastka z (1575 / 16)
po skróceniu wyjdzie
30 / √(1575/16)
30 podzielone przez pierwiastek z (1575 / 16), co w przybliżeniu da promień okręgu
R≈3,0237157841
Można pole trójkąta abc skrócić wcześniej do formy
P = √(1575/16) = √1575 / 4 = √(225*7 / 4 =
15 √7 / 4
zwłaszcza, że przy liczeniu promienia R w liczniku będziemy mieć 120, a w mianowniku będziemy mnożyć przez 4
Tak więc
R = 120 / 15√7
a po skróceniu 120 i 15 do prostej ósemki w liczniku ( 120/15=8 ) i pozostawiając proste √7 w mianowniku
WYCHODZI BARDZO ŁADNE ROZWIĄZANIE
R = 8 / √7
co po podstawieniu do wzoru na pole koła, prowadzi do
BARDZIEJ ŁADNEGO ROZWIĄZANIA
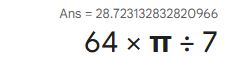
P ≈ 28.7231328328…
…które niestety niespójne jest z
rozwiązaniem @joko 28,26
rozwiązaniem @benasek 28,65
ps. zapisy i obliczenia na brudno nie nadają się do publikacji. Być może po przepisaniu na czysto będą się nadawały, w co jednak osobiście wątpię
ojej…
Też miałem taką minę jak to zobaczyłem 
1 polubienie
To byłoby nawet technicznie i matematycznie możliwe 
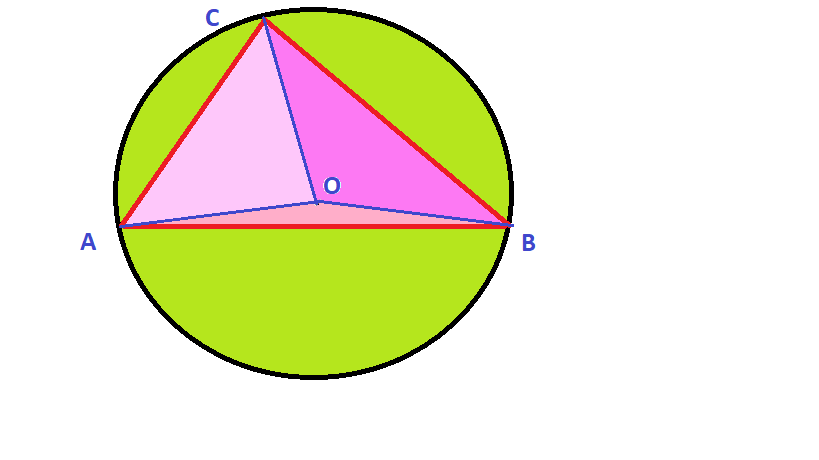
Oznaczmy wierzchołki trójkąta jako punkty A, B i C
Jedną z metod podanych wyżej obliczamy promień opisanego na tym trójkącie okręgu, a następnie pole powierzchni koła o tym promieniu.
TU OBLICZENIA MOZNABY ZAKOŃCZYĆ, BO ZADANIE ZOSTAŁO WYKONANE, ALE MY CHCEMY DOKONAĆ TEGO METODĄ NA OKONKA
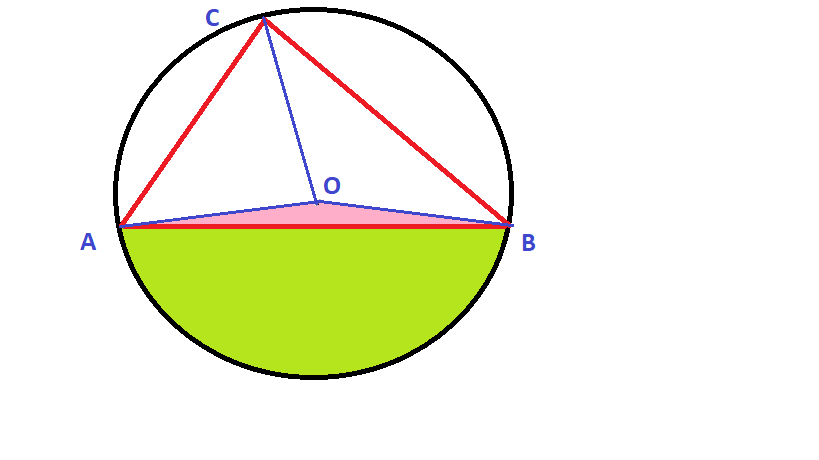
Oznaczmy środek tego okręgu jako punkt O
Po wyznaczeniu promienia okręgu mamy wszystkie dane, aby obliczyć kąty trzech trójkątów składających się na trójkąt ABC.
Odcinki AO, BO i CO są sobie równe i równe promieniowi R okręgu.
Odcinki AC, CB i AB też są znane i wynoszą odpowiednio 4. 5 i 6.
Znając kąt AOB obliczmy pole powierzchni wycinka koła ograniczonego punktami A, O i B
Znając długości boków trójkąta AOB (oznaczonego na rysunku kolorem różowym), obliczymy jego powierzchnię.
Teraz powierzchnię trójkąta AOB odejmijmy od powierzchni wycinka koła wyznaczonego punktami A, O i B.
Otrzymamy pole powierzchni fragmentu koła od
ciętego cięciwą AB (oznaczonego na rysunku kolorem zielonym).
Proste, prawda? 
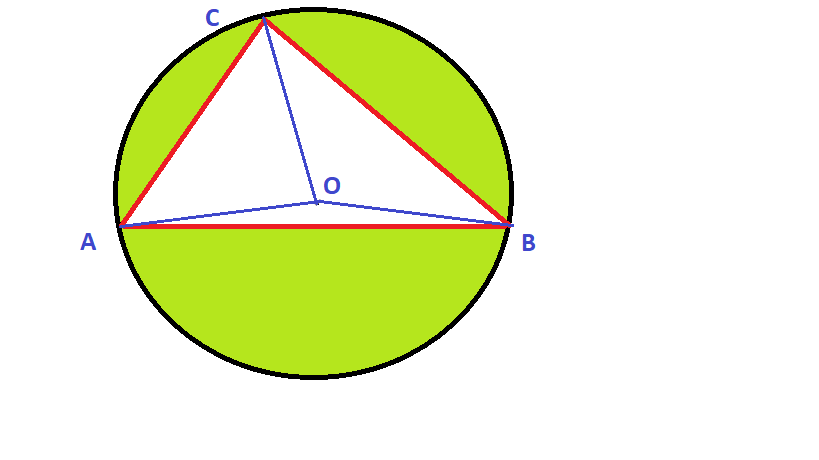
To samo robimy z trójkątami AOC i BOC
oraz odpowiednio z wycinkami koła ograniczonymi punktami A. O i C oraz B, O i C.
Odejmujemy obliczone wartości, bo Metoda na okonka tego wymaga.
W wyniku skomplikowanych obliczeń otrzymaliśmy potrzebne nam pola trzech fragmentów koła, które zostały odcięte cięciwami AB, BC i CA (oznaczone na rysunku kolorem zielonym).
Połowa już za nami. Uff.
Skoro już policzyliśmy i dodaliśmy do siebie pola trzech fragmentów koła odciętych cięciwami, do pełni szczęścia potrzebne jest nam pole trójkąta ABC (oznaczonego na rysunku kolorami różowymi).
Wartość tę możemy:
- zerżnąć na bezczela z wyników powyżej
- obliczyć i dodać do siebie pola trzech trójkątów AOB, BOC i COA które łącznie tworzą duży trójkąt ABC.
Obie metody są skuteczne
Skoro posiadamy już pole trójkąta ABC oraz pola trzech fragmentów koła odciętych ciaciwami AB, BC i CA, metoda na okonka wymaga, aby te wartości zsumować, nie zważając oczywiście na to, że krok wcześniej wartości te odejmowaliśmy.
Cóż, Metoda na okonka nie jest łatwa 
Voilà.
W wyniku tych perturbacji otrzymaliśmy pole koła opisanego na trójkącie ABC o bokach 4, 5 i 6, które w dalszym ciągu wynosi
P ≈ 28.7231328328…
1 polubienie