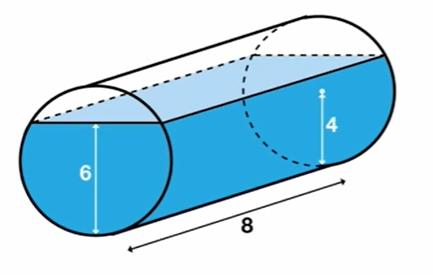
Do baniaka o kształcie walca wlano wodę. Baniak to prosta konstrukcja o średnicy 8 metrów i wysokości 8 metrów.
I na tym prostota się skonczyła 
Baniak wziął się i przewrócił się 
I leży. Poziom wody w leżącym baniaku to równo 6 metrów.
ILE WODY JEST W BANIAKU ???
Pi razy sześcian.i tyle samo
W/g Perplexity:183,1 metrów sześciennych wody
W/g CzatGPT:≈323,5m3.
A według mnie: Nie mam pojęcia!
Ale bieda
323,5 m sześc.
323,36 m sześciennych
Ale te AI oporne.Wyliczyło mi,podało wzory i pyta czy chcę wynik.
Dopiero jak odpisałem:Chyżej waść,ja nie młodnieję.Dawaj wynik - to łaskawie podało.
Zdecydowanie wolę z ludźmi gadać,bo z nieczłowiekami ciężko jakoś…
W jakim celu więc publikujesz to, co wygenerowała yntelygencja
Nagroda w postaci zakazu uczestnictwa w trzech kolejnych edycjach zagadek została przez Imć @Bingola zignorowana, wobec czego zwiększamy wartość nagrody o kolejne trzy edycje. Razem sześć
A ićta, yaya se robita.
Człowiek poważnie podchodzi do problemu a tu łapieta go za słówka ignorując tok myślenia.
Nie mam zamiaru pisać do każdego wyrazu jego definicjii i objaśnień.
Ale żeby nie było, nie gniewam się, wracam do roboty…
Proszę @okonek o wstawienie tego komentarza do pytania z maratonem.
Ciekawym, jak to policzylście???
Pitagorasem, czy na skróty wg wzoru z neta🤔
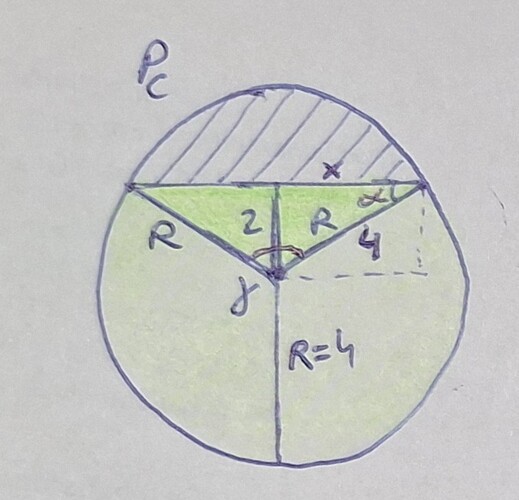
Trzeba najpierw obliczyć zielone pole, czyli część koła z którym będzie się stykała woda. Jest ono równe wycinkowi koła + pole tych dwóch ciemniejszych trójkątów.
Pole wycinka to (kąt gamma / 360) × pole całego koła
Pole trójkątów tez się da, bo mamy boki. Mamy również kąty, bo z definicji sinusa go obliczymy.
Zielone pole mnożymy przez wysokosc baniaka
Mam dalej tłumaczyć?
Dokładnie tak samo ja rozwiązywałem, ale nie bedę wrzucał swoich bazgrołów 
OK Profesory @benasek i @Bingola
Zagadka bonusowa za całe zero punktów
Pojawia się Herkules (albo lepiej dwóch) i stawiają baniak pionowo.
JAK WYSOKI BĘDZIE SŁUP WODY W PIONOWO POSTAWIONYM BANIAKU ???
6,44 m mi wyszło.
Dzielimy te wcześniejsze “moje” zielone pole przez pole całego koła i mnożymy przez 8m.
Pion jesli na skutek Waszych obliczen sie nie zmieni? Pole grawitacyjne? 
Koleżanko, nie wymyślać, nie kombinować, za to skupić się i sprawdzić, czy się benasek nie machnął… 
A czy ja samobójca?
Ło panie!
Nie na trzeźwo
Skoro tak wyszło, to teraz nasuwa się pytanie, kiedy Herkulesy zaczną się nudzić.
…
Nie trzeba było długo czekać i Herkulesy zaczynają rozrabiać.
Usunęli górną pokrywę baniaka i teraz jeden przechyla, a drugi podpiera.
POD JAKIM KĄTEM NALEŻY PRZECHYLIĆ BANIAK Z WODĄ, TAK BY PODPIERAJĄCEMU HERKULESOWI ZACZĘŁO LAĆ SIĘ NA GŁOWĘ ???
