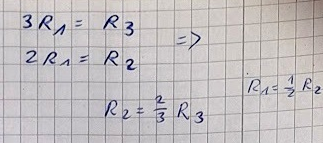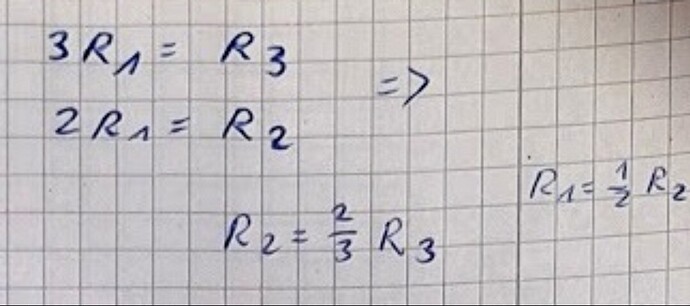.dam Ci sera na pierogi 
1 polubienie
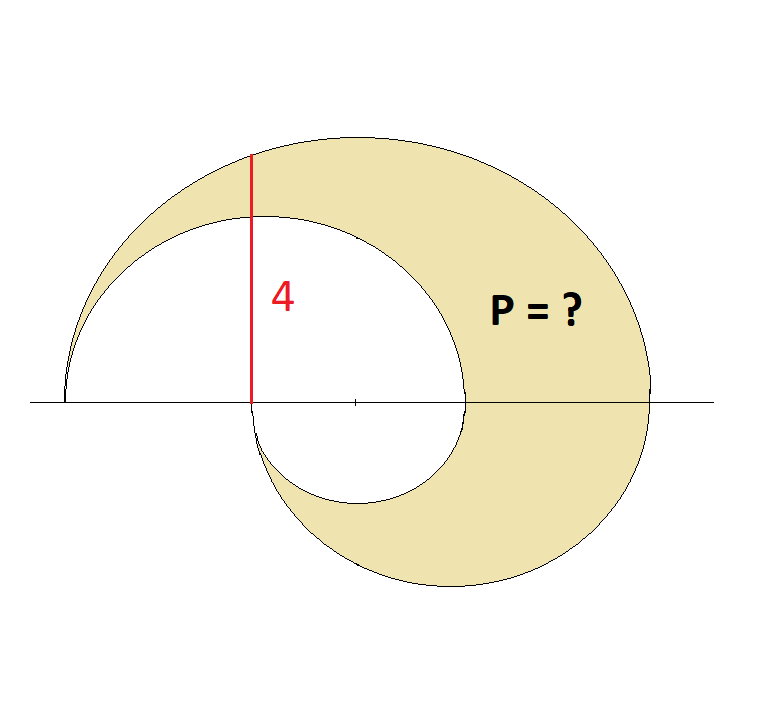
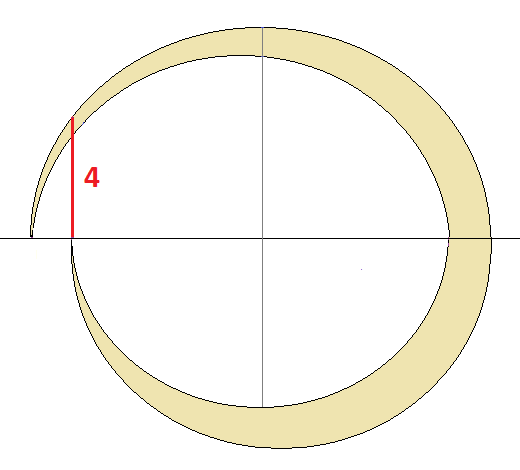
Czy wszystkie krzywe na tym rysunku są półokręgami? Pytam, bo wyglądają na podobne do elipsy albo nawet są elipsami.
2 polubienia
Tak, to półokręgi. Najmniejszy i największy z nich mają wspólny środek.
Zadanie z elipsami byłoby chyba nierozwiązywalne. Jest wprawdzie wzór na pole elipsy, ale w tym zadaniu mielibyśmy zbyt mało danych, aby wydedukować długości wszystkich osi.
1 polubienie
To w takiej sytuacji jest to bardzo fajne, niezbyt trudne zadanko, przynajmniej w mojej ocenie. Zrobiłem je, mam wynik, wierzę, że dobry, ale poczekam, niech i inni się pobawią. Dziś i jutro do późnego popołudnia mam sporo do zrobienia w tym jedną podróż. Gdy wrócę, zobaczymy, czy ktoś dał radę.
2 polubienia
Wyślij na PW
Zmierzyłem długości osi dwóch elips. Różnica to 2 piksele
Kot dostrzegł różnicę dwóch pikseli w promieniach półokręgów 
To wrócimy do tego jak wrócę…
2 polubienia
Inni ślimaczą się z zadaniem
1 polubienie
Powierzchnia P = 25,13
Poniżej przy okazji zrobione zadanko “Równouprawnienie”
Notatki obliczeniowe “z marszu” więc, jak ktoś ma pytania co do tych bazgrołów, niech pyta.
1 polubienie
Z jakiej matematycznej logiki wynikają te założenia?
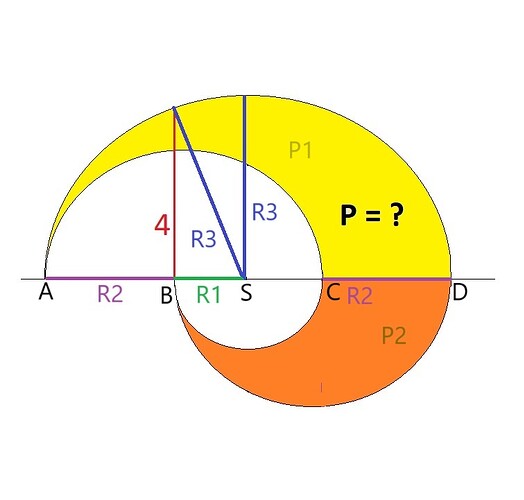
Dlaczego R3 jest trzykrotnością R1, a R2 to dwukrotność R1 ???
Twoje obliczenia opierają się na założeniu, że R2 to dwie/trzecie R3.
Skąd wynika ta zależność.??
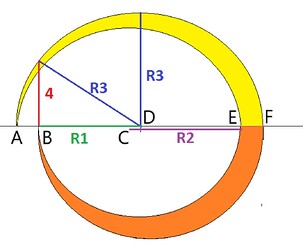
Narysowałem ślimaka ponownie w innych proporcjach.
Serduszko daje w ciemno za te wiry kosmiczne … 
1 polubienie
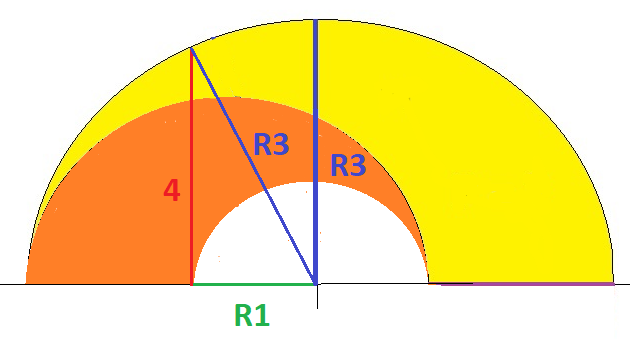
Przy obliczaniu założyłem, że odcinki AB, BC i CD są równe. Założyłem również, że ten odcinek z wartością 4 wychodzi z B, który jest środkiem średniego koła. Tak przynajmniej można zrozumieć z przedstawionego przez Ciebie rysunku. Jeśli jednak tak nie musi być, jak w Twoim kolejnym przykładzie, to prawdopodobnie też się to da obliczyć a pewne wartości (których nie znamy) się poskracają. Tego na razie nie wiem, bo wspomnianego następnego przypadku nie analizowałem. Gdy znajdę trochę czasu, wrócę pewnie do tego w zaciszu domowym.
Czyżby na tym portalu nie było więcej osób, które by to próbowały rozwiązać?
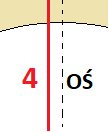
W zadaniu nie ma mowy o środku średniego koła. Oś o długości 4 nie jest osią tego koła. Trochę źle narysowałem, ale na monitorze komputera jest to bardziej widoczne.
Poprzednio obliczyłem to zadanie dla przypadku szczególnego o którym wczesniej wspomniałem. Poniżej masz rozwiazanie dla przypadku ogólnego i myślę, ze o to Ci chodzi.
1 polubienie
Cóż za uderzające podobieństwo
Który ze ślimaków jest więc przypadkiem szczególnym, skoro oba mają 8π powierzchni
1 polubienie
Ten przy którym założyłem poniższe proporcje promieni
Jednak jak wynika z drugiego rozwiązania, promień sredniego okręgu nie ma znaczenia. Tak zresztą wczesniej podejrzewałem.
Jakkolwiek i cokolwiek byś nie zakładał, powierzchnia ślimaka zawsze będzie 8 π, dopóki pionowy odcinek będzie miał długość 4.
Właśnie to wykazalem w ostatnim rozwiązaniu 
1 polubienie
Odkryłem to, porównując moje rozwiązanie z Twoim pierwszym rozwiązaniem z punktem B jako środek średniego koła. Później narysowałem innego ślimaka, a wynik się nie zmieniał.
Nie znaczy to oczywiście, że wszystkie ślimaki we Wszechświecie mają powierzchnię 8 π, ale to jest chyba jasne 
Moje rozwiązanie mieści się w kilku linijkach.
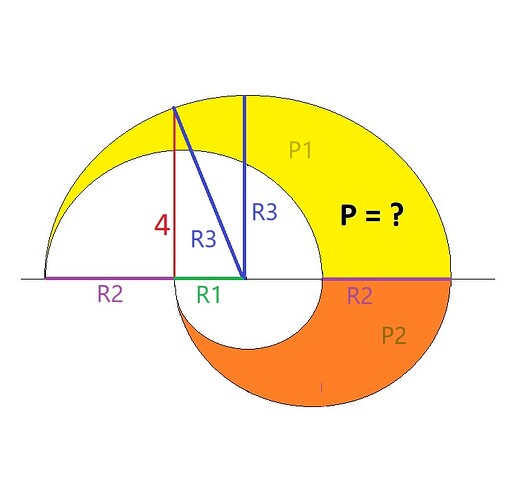
Skróciłem więc całkowicie pola średniego półkola, bo są identyczne.
Pole półkola o średnicy BD dodajemy do pola całości, a pole półkola AC odejmujemy. Wynikiem jest zero, a więc pole powierzchni średniego koła można w obliczeniach pominąć.
Pole powierzchni ślimaka więc, to
pole półkola o promieniu R3 MINUS pole półkola o promieniu R1.
R3² = 4² + R1² = 16 + R1² => 16 = R3² - R1²
P = (π * R3²) /2 - (π * R1²) /2 => π/2 * (R3² - R1²) => π/2 * 16
P = 8π
Zamykając ślimaczny temat, można stwierdzić z całą stanowczością, że o ślimakach wiemy już wszystko 
1 polubienie